MEASUREMENT -A-LEVEL

GENERAL

SI Units

• “Systeme International”, or SI Units, is a standardised system of measurement based on internationally agreed definitions.
• It has 7 Base Units, from which all other units are derived:
  • Metre (m) - Length
  • Kilogram (Kg) - Mass
  Second (s) - Time
  • Kelvin (°K) - temperature
  • Ampere (A) - Current
  • Candela (Cd) - Luminous Intensity
  • Mole (mol) - Amount of a substance
• All the base units have standard definition, for example, the metre is the distance travelled by light in a vacuum in seconds.
• Other units are derived from the base units. For example:
  • Velocity (ms^-1)
  • Acceleration (ms^-2)
  • Density (Kgm^-2)
• Some of the derived units also have their own special unit names. For example:
  • Coulomb (C) - (As) Charge
  • Pascal (Pa) - (Kgm^-1s^-2) Pressure
  • Ohms (Ω) - (Kgm²s^-3A^-2) Resistence

Prefixes

• In order to make working with large or small numbers more convenient, a system of prefixes is used, where the unit is multiplied by a certain power of ten:
  • Yotta (Y) - 10²⁴
  • Zetta (Z) - 10²¹
  • Exa (E) - 10¹⁸
  • Peta (P) - 10¹⁵
  • Tera (T) - 10¹²
  • Giga (G) - 10⁹
  • Mega (M) - 10⁶
  • Kilo (k) - 10³
  • Milli (m) - 10^-3
  • Micro (μ) - 10^-6
  • Nano (n) - 10^-9
  • Pico (p) - 10^-12
  • Femto (f) - 10^-15
  • Atto (a) - 10^-18
  • Zepto (z) - 10^-21
  • Yocto (y) - 10^-24
• In addition, these prefixes are also used:
  
  • Hecto (h) - 10²
  • Deca (da) - 10¹
  • Deci (d) - 10-^-1
  • Centi (c) - 10^-2
• For example, 0.005 A can be written as 5 mA, and 6900000000000000000000000 m can be written as 6.9 Ym. 

MATERIAL

• Material Properties

• There are a variety of terms that can be used to describe a material.
  • Hard - Can scratch or indent, and withstands being scratched
  • Brittle - Breaks without plastic deformation
  • Ductile - Can be drawn into a wire
  • Malleable - Can be reshaped
  • Elastic - Returns to its original shape after being deformed
  • Plastic - Does not return to its original shape after being deformed
  • Strong - Widthstands large static loads without breaking
  • Tough - Withstands large dynamic loads without breaking
  • Stiff - Resists deforming by tension or compression
• Strong materials can withstand large static loads whilst tough materials can withstand large dynamic loads.
• Tensile Strength is the force that is used to stretch a sample at any time while the Ultimate Tensile Strength is the force required to break it.
•  

  Hooke’s Law

  • Hooke’s Law states that, for certain elastic materials, force is proportional to extension, when a sample is stretched. This means that the extension of the sample increases linearly with the amount of force applied. Materials that obey Hooke’s law are called Hookean Materials. Springs behave like Hookean Materials.
  • Hooke’s law can be written as $F=kx$, where $F$ is Force, $x$ is extension, and $k$ is the Stiffness Constant of the sample. The stiffness constant describes the stiffness of a material, and is measured in $N{m}^{-1}$ (or $Kg{s}^{-2}$).

  $$F=kx$$
  

  • Hooke’s law can be demonstrated with the use of Force-Extension graphs.

  
  
  

  

  A material obeying Hooke’s Law. The graph shows how force (the vertical axis) changes with extension (the horizontal axis).

  
  

  • However, no sample follows Hooke’s law indefinitely, and there comes a point, called the Limit of Proportionality, where there is no longer a linear relationship between force and extension. After yet more force is applied, the Elastic Limit will be reached. This means that the sample will no longer return to its original shape when the force ceases to be present. Eventually, the force will become so great that the material snaps. This is called the Yeild Point.

  
  
  

  

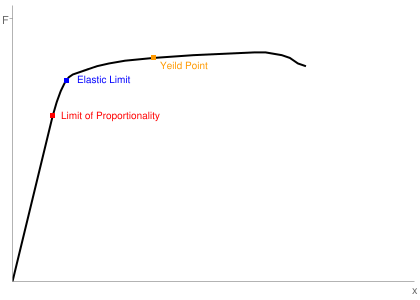
  A material reaching its limit of proportionality and ceasing to obey Hooke’s Law

  • Before the elastic limit is reached, the sample is experiencing Elastic Deformation, where it will return to its original shape when the load (force) has been removed. However, once the material passes that point, it experienced Plastic Deformation, where its shape is permanently changed.
  • If two springs are used in series, the effective stiffness constant of both of them is less than either of them. In fact, it can be worked out by the formula: $\genfrac{}{}{0ex}{}{1}{k^{\text{eq}}}=\genfrac{}{}{0ex}{}{1}{k^1}+\genfrac{}{}{0ex}{}{1}{k^2}$. If two springs are in parallel, their effective stiffness constant is greater: $k^{\text{eq}}=k^1+k^2$.

Elastic Strain Energy

• Up to the elastic limit of a sample, all the work done in stretching it is stored potential energy, or Elastic Strain Energy. This value can be determined by calculating the area under the the force-extension graph. If the sample obeys Hooke’s Law, and is below the elastic limit, the Elastic Strain Energy can be calculated by the formula:

E = ½Fx

• Or, since F = kx (where k is the stiffness constant of the sample):

E = ½kx²

…

• Some force-extension graphs have two curves, one measured when force was being applied (loading) and one where that force was being removed (unloading). The unloading curve may be below the loading curve, which would mean that less energy is given out when a force is removed from the sample than was put in, as the area under the unloading curve is less than that of the loading curve. This is because some of the energy put into the material was transferred as waste energy, like heat.

Young Modulus

• The value of a Stiffness Constant only applies to a certain sample. F_or example, a longer piece of the same material would have a lower stiffness constant._ The Young Modulus on the other hand is a material property, meaning it can be applied to all samples of the same material. It is calculated by the formula:

Stress and Strain

• Stress is a measure of the force applied per unit cross-sectional area of a material. It is measured in Pascals (Pa, or Nm^-2, or Kgm^-1s^-2 if you want to be pedantic). It is hence calculated by the formula:

• Strain is the change in length relative to original length. It has no units since it is the ratio of two lengths. It is calculated by the formula:

• A stress on a material causes a strain.

• For a material, a stress-strain graph can be drawn. The gradient of this graph is then the Young Modulus. The Young Modulus is also measured in Pascals. By finding the area under a stress-strain graph, it is possible to work out the energy stored per unit volume in a material.

…

• The Young Modulus, being a material property as it is, can be used to generalise the elastic properties of a material. This is very useful, for example, in working with seat belts, as it important to be able to calculate how far they will stretch for any length or thickness.

Fluid Flow

• A Fluid is substance that can flow, like a Liquid or a Gas. The flow of a fluid can be represented by Streamlines, which are ‘fluid elements’ that move relative to each other.
• In Laminar Flow, all the fluid elements flow in the same direction, and none of the streamlines cross over. It usually occurs at lower velocities and with streamlined objects. The word ‘laminar’ means flow in layers, and it is as if there are layers of fluid sliding over each other. In laminar flow, the ‘layers’ towards the middle tend to flow faster.
• Turbulent Flow occurs at higher velocities or with non streamlined objects, when the flow lines become chaotic and mixed up. Eddies - small whirlpools - form where the flow gets mixed up.

Upthrust and Viscosity

Density

• Density, ρ is defined as the mass per unit volume. It is measured in Kgm^-3.

Density: Mass per unit volume

Upthrust

• A fluid will exert a force upward on a body if it is partly or wholly submerged within it. This is because the deeper into a fluid you go, the greater the weight of it and so the greater the pressure. This difference in pressure between the top and the bottom of the object produces an upward force on it. This is called Upthrust.
• According to Archimedes’ Principle, the upthrust on an object in a fluid is equal to the weight of the fluid displaced. So the volume of the object multiplied by the density of the fluid.

Upthrust = Weight of Fluid Displaced

Viscosity

• In a fluid, each ‘layer’ experts a force of friction of each other ‘layer’. This frictional force is also present when solid object moves through a liquid. This force is termed Viscous Drag. Viscous Drag is greater in Turbulent Flow than Laminar Flow.
• The size of the Viscous Drag in a fluid depends on the (coefficient of) Viscosity of that fluid. Viscosity is given the letter η and is measured in Kgm^-2s or Pa s. The greater the Viscosity, the greater the Viscous Drag.
• In most liquids, Viscosity decreases as temperature increases, whereas in most gases, Viscosity increases as temperature increases. It is therefore important to always measure the temperature of a fluid when measuring Viscosity.

• It is possible to calculate the drag force exerted on a spherical object in a fluid using Stoke’s Law:

F = 6πηrv

• Stoke’s Law assumes Laminar Flow, and so low velocities.
• In this equation, v represents Terminal Velocity. This means that the forces acting on the object are balanced. This means that is it possible to form an equation be equating Weight with Upthrust and Viscous Drag (or, in the case of Upward Motion, Upthrust with Weight and Viscous Drag).

 

Current, Voltage and Power

• Electricity is the flow of electric charge. We can describe the flow of electric charge in several ways. These include the quantities Current, Voltage and Power.

Current

• Current (I) is the rate of flow of Charge Carriers, such as electrons. Current is usually thought of as moving in the direction of positive charge, so from the positive power supply to the negative. However, since in metals it is electrons that carry electric charge, the actually flow is opposite to the way in which we think of it.

• Current it the the amount of Charge, Q that passes a point in a set time, t. It is measured in Amps (A), and charge is measured in Coulombs (C). Since Amps are SI base units, Coulombs are defined as A×s, As.

Voltage

• Voltage (V) or Potential Difference (p.d.) is a measure of the Energy transferred per Charge Carrier between two points.

• Voltage is the Energy, E per Charge, Q. Voltage is measured in Volts (V), which is defined as one Joule per Coulomb. Voltage can be defined in base units as Kgm²s^-3A^-1.

Power

• Power (P) is the rate of Energy transfer. It is measured in watts (W), where one watt is defined as one Joule per Second. Hence watts can be expressed in base units as Kgm²s^-3

• From this definition of Power, we can substitute the algebraic definitions above to produce a variety of other formulae, including ‘Power = Current × Voltage’

• Ohm’s Law states that ‘Voltage = Current × Resistance’. We can use this to produce two more definitions of Power.

Resistance and Resistivity

• Resistance it the opposition to the passage of current within a component. The Resistance of a component decides how much voltage will be dropped across it for a particular current.
• Resistance is measured in Ohms (Ω). According to Ohm’s Law, voltage is the product of current and resistance. Therefore Ohms can be expressed in base units as $\mathrm{K}\mathrm{g}{\mathrm{m}}^2{\mathrm{s}}^{-3}{\mathrm{A}}^{-2}$.

$$V=IR$$

• Everything has Resistance, because everything has some opposition to the flow of Electric Charge. Components whose sole purpose is to provide a Resistance of a certain value are called Resistors.

…

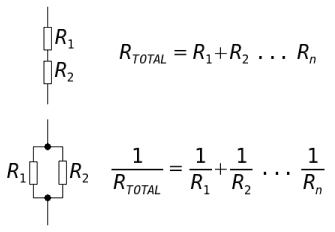
• When Resistors are connected in Series, the total Resistance across them will be equal to the sum of each Resistor value. The total voltage will be equal to the sum of the voltages across each Resistor. This rule will also apply for other components.

When Resistors are connected in Parallel, the reciprocal of the total resistance will be equal the sum of the reciprocals of each Resistor Resistance. The total voltage dropped will be the same as the voltages dropped across all the individual Resistors.

…

Resistivity

• Resistance is a Sample Constant, so is specific to individual components. However, there is a Material Constant that can be used to find the Resistance of any component of a specific material. This is Resistivity. Together with the length and cross-sectional area of a sample, it can calculate its resistance.
• Resistivity is given the symbol ρ and is measured in Ohm Meters (Ωm, or Kgm³s^-3A^-2 in base units).
• For example, copper has a Resistivity of 1.68 ×10^-8 Ωm, and Germanium 4.6 ×10^-1 Ωm.
• The Resistance of a material of Resistivity ρ, length l and cross-sectional area A is calculated by the formula: